Molecule Generation#
Molecular graph generation is a fundamental problem for drug discovery and has been attracting growing attention. The problem is challenging since it requires not only generating chemically valid molecular structures but also optimizing their chemical properties in the meantime.
In this tutorial, we will implement two graph generative models GCPN and GraphAF. We first pretrain both models on ZINC250k dataset. Starting from the pretrained checkpoint, we finetune both models with reinforcement learning to optimize two properties (i.e., QED and penalized logP score) of generated molecules.
Prepare the Pretraining Dataset#
We use ZINC250k dataset for pretraining. The dataset contains 250,000 drug-like molecules with a maximum atom number of 38. It has 9 atom types and 3 edge types.
First, let’s donwload, load, and preprocess the dataset, which takes about 3-5 minutes. You are encouraged to dump the preprocessed dataset to save the time for future use.
import torch
from torchdrug import datasets
dataset = datasets.ZINC250k("~/molecule-datasets/", kekulize=True,
atom_feature="symbol")
# with open("path_to_dump/zinc250k.pkl", "wb") as fout:
# pickle.dump(dataset, fout)
# with open("path_to_dump/zinc250k.pkl", "rb") as fin:
# dataset = pickle.load(fin)
Define the Model: GCPN#
The model consists of two parts, a graph representation model and a graph generative
module. We define a Relational Graph Convolutional Networks (RGCN) as our
representation model. We use the module
GCPNGeneration as the training task
for GCPN.
from torchdrug import core, models, tasks
model = models.RGCN(input_dim=dataset.node_feature_dim,
num_relation=dataset.num_bond_type,
hidden_dims=[256, 256, 256, 256], batch_norm=False)
task = tasks.GCPNGeneration(model, dataset.atom_types, max_edge_unroll=12,
max_node=38, criterion="nll")
Pretraining and Generation: GCPN#
Now we can train our model. We setup an optimizer for our model, and put everything together into an Engine instance. Here we only train the model for 1 epoch, and then save the pretrained model into a directory.
from torch import nn, optim
optimizer = optim.Adam(task.parameters(), lr = 1e-3)
solver = core.Engine(task, dataset, None, None, optimizer,
gpus=(0,), batch_size=128, log_interval=10)
solver.train(num_epoch=1)
solver.save("path_to_dump/graphgeneration/gcpn_zinc250k_1epoch.pkl")
During the pretraining procedure, we may obtain some logs as follows, which report the accuracy of action predictions.
edge acc: 0.896366
edge loss: 0.234644
node1 acc: 0.596209
node1 loss: 1.04997
node2 acc: 0.747235
node2 loss: 0.723717
stop acc: 0.849681
stop bce loss: 0.247942
total loss: 2.25627
After the model is pretrained, we can load the parameters from the checkpoint as follows. Let’s generate some small molecules from the pretrained GCPN model.
solver.load("path_to_dump/graphgeneration/gcpn_zinc250k_1epoch.pkl")
results = task.generate(num_sample=32, max_resample=5)
print(results.to_smiles())
The results are as follows:
C=S(C)CC(=O)NC(CCN)CCCC
CCN(C)C1(C2NC2=O)CCCC1C
CC1=CC=CC=C1C(=O)N1CC1CS
CN=NC1=NC=CC2=CC=C(C=C2)CCNC(=O)C1
CC(CC(=O)NC1=CC=C(N)C2=CC=CC=C12)C1=CC=CC=C1
...
Let’s visualize some generated molecules.
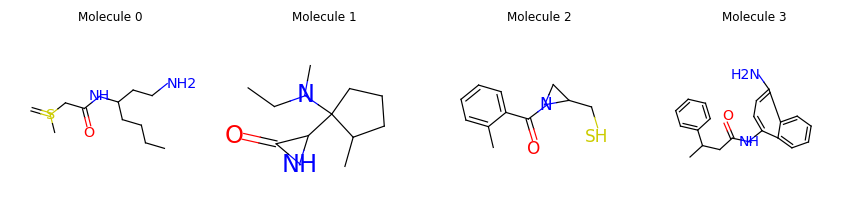
Goal-Directed Molecule Generation with Reinforcement Learning: GCPN#
For drug discovery, we need to optimize the chemical properties of generated molecules. In this part, we introduce how to fine-tune the graph generative model with reinforcement learning to optimize the properties of generated molecules. We implemented the Proximal Policy Optimization (PPO) algorithm for both GCPN and GraphAF. To finetune the pretrained model with reinforcement learning, we only need to modify several lines of code in the task initialization. We provide all the codes for finetuning in the following segment.
For Penalized logP optimization, the code is as follows:
import torch
from torchdrug import core, datasets, models, tasks
from torch import nn, optim
from collections import defaultdict
dataset = datasets.ZINC250k("~/molecule-datasets/", kekulize=True,
atom_feature="symbol")
model = models.RGCN(input_dim=dataset.node_feature_dim,
num_relation=dataset.num_bond_type,
hidden_dims=[256, 256, 256, 256], batch_norm=False)
task = tasks.GCPNGeneration(model, dataset.atom_types,
max_edge_unroll=12, max_node=38,
task="plogp", criterion="ppo",
reward_temperature=1,
agent_update_interval=3, gamma=0.9)
optimizer = optim.Adam(task.parameters(), lr=1e-5)
solver = core.Engine(task, dataset, None, None, optimizer,
gpus=(0,), batch_size=16, log_interval=10)
solver.load("path_to_dump/graphgeneration/gcpn_zinc250k_1epoch.pkl",
load_optimizer=False)
# RL finetuning
solver.train(num_epoch=10)
solver.save("path_to_dump/graphgeneration/gcpn_zinc250k_1epoch_finetune.pkl")
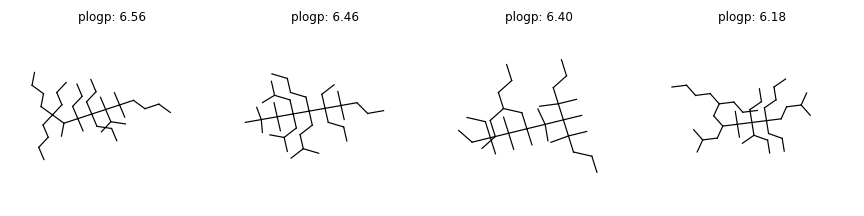
The results are as follows:
(6.56, 'CCCCC(CCC)(CCCC)C(C)C(C)(CCC)C(CCC)(CCC)C(C)(C(C)C)C(C)(C)CCCC')
(6.46, 'CCCCC(CCC(C)C)(C(CC)(CCC)C(C)(C)CCC)C(CC(C)C)(CC(C)C)C(C)(C)C(C)(C)C')
(6.40, 'CCCC(CCC)CC(C)(C(C)(C)C(C)(CC)CC)C(C)(C)C(C)(C(C)(C)CCC)C(C)(C)CCC')
(6.18, 'CCCCC(CCC)CC(CC(C)C)C(C)(C)C(CCC)(C(C)CC)C(CCC)(CCCC)CCC(C)C')
...
Let’s visualize some molecules with large Penalized logP scores (> 6).
For QED optimization, the task initialization is as follows:
task = tasks.GCPNGeneration(model, dataset.atom_types,
max_edge_unroll=12, max_node=38,
task="qed", criterion=("ppo", "nll"),
reward_temperature=1,
agent_update_interval=3, gamma=0.9)
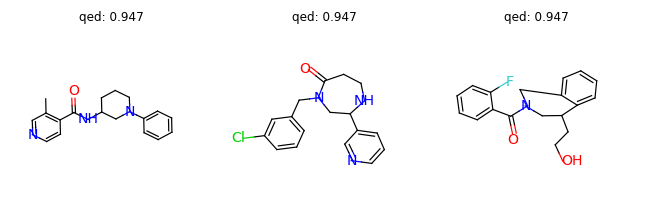
The results are as follows:
(0.948, 'C1=CC=C(CNC2=NC=NCC3=CN2C(C2=COCC2)=C3)C=C1')
(0.948, 'CCC1=CC=CC=C1NC(=O)C12CC(=O)N(C1)C1=CC=CC=C12')
(0.947, 'O=C1CCNC(C2=CC=CN=C2)CN1CC1=CC=CC(Cl)=C1')
(0.947, 'CC1=C(C(=O)NC2CCCN(C3=CC=CC=C3)C2)C=CN=C1')
(0.947, 'CCNC1CCC2=CC=CC(=C2)N(C(=O)C2=CC=CC=N2)C1')
(0.946, 'O=C(C1=CC=CC=C1F)N1CC2=CC=CC=C2C(CCO)C1')
...
Let’s visualize some molecules with large QED scores (> 0.945).
Define the Model: GraphAF#
The model consists of two parts, a graph representation model and a graph generative
module. We define a Relational Graph Convolutional Networks (RGCN) as our
representation model. We use the module
AutoregressiveGeneration as
the training task for GraphAF. The task consists of a node flow model and an edge
flow model, which define invertible mapping between node / edge types and noise
distributions.
from torchdrug import core, models, tasks
from torchdrug.layers import distribution
model = models.RGCN(input_dim=dataset.num_atom_type,
num_relation=dataset.num_bond_type,
hidden_dims=[256, 256, 256], batch_norm=True)
num_atom_type = dataset.num_atom_type
# add one class for non-edge
num_bond_type = dataset.num_bond_type + 1
node_prior = distribution.IndependentGaussian(torch.zeros(num_atom_type),
torch.ones(num_atom_type))
edge_prior = distribution.IndependentGaussian(torch.zeros(num_bond_type),
torch.ones(num_bond_type))
node_flow = models.GraphAF(model, node_prior, num_layer=12)
edge_flow = models.GraphAF(model, edge_prior, use_edge=True, num_layer=12)
task = tasks.AutoregressiveGeneration(node_flow, edge_flow,
max_node=38, max_edge_unroll=12,
criterion="nll")
Pretraining and Generation: GraphAF#
Now we can train our model. We setup an optimizer for our model, and put everything together into an Engine instance. Here we train the model for 10 epochs, and then save the pretrained model into a directory.
from torch import nn, optim
optimizer = optim.Adam(task.parameters(), lr = 1e-3)
solver = core.Engine(task, dataset, None, None, optimizer,
gpus=(0,), batch_size=128, log_interval=10)
solver.train(num_epoch=10)
solver.save("path_to_dump/graphgeneration/graphaf_zinc250k_10epoch.pkl")
After the model is pretrained, we can load the parameters from the checkpoint. Let’s then generate some small molecules from the pretrained GraphAF model.
from collections import defaultdict
solver.load("path_to_dump/graphgeneration/graphaf_zinc250k_10epoch.pkl")
results = task.generate(num_sample=32)
print(results.to_smiles())
The results are as follows:
CC(C)C=C(Cl)NC1=CC=CC=C1
CCOC(=NNCC(C=CC(C)=CC=CC=CC(C)=CC=O)(CO)CO)C(C)C
CCC(C)(NC(C)Cl)C1=CC=CNC#CO1
O=C1NC2=CC(=CC=S)C1=CC=CC=C2
C=[SH]1(CC)C#SC(=NC(C)=C(C)Cl)C1N
...
Finetuning: GraphAF#
For Penalized logP optimization, the code is as follows:
import torch
from torchdrug import core, datasets, models, tasks
from torchdrug.layers import distribution
from torch import nn, optim
from collections import defaultdict
dataset = datasets.ZINC250k("~/molecule-datasets/",
kekulize=True,
atom_feature="symbol")
model = models.RGCN(input_dim=dataset.num_atom_type,
num_relation=dataset.num_bond_type,
hidden_dims=[256, 256, 256], batch_norm=True)
num_atom_type = dataset.num_atom_type
# add one class for non-edge
num_bond_type = dataset.num_bond_type + 1
node_prior = distribution.IndependentGaussian(torch.zeros(num_atom_type),
torch.ones(num_atom_type))
edge_prior = distribution.IndependentGaussian(torch.zeros(num_bond_type),
torch.ones(num_bond_type))
node_flow = models.GraphAF(model, node_prior, num_layer=12)
edge_flow = models.GraphAF(model, edge_prior, use_edge=True, num_layer=12)
task = tasks.AutoregressiveGeneration(node_flow, edge_flow,
max_node=38, max_edge_unroll=12,
task="plogp", criterion="ppo",
reward_temperature=20, baseline_momentum=0.9,
agent_update_interval=5, gamma=0.9)
optimizer = optim.Adam(task.parameters(), lr=1e-5)
solver = core.Engine(task, dataset, None, None, optimizer,
gpus=(0,), batch_size=64, log_interval=10)
solver.load("path_to_dump/graphgeneration/graphaf_zinc250k_10epoch.pkl",
load_optimizer=False)
# RL finetuning
solver.train(num_epoch=10)
solver.save("path_to_dump/graphgeneration/graphaf_zinc250k_10epoch_finetune.pkl")
The results are as follows:
(5.63, 'CC=CC=CC=CC=CC=CC=CC=CC=CC=CC=CC=CC=CC=CC=CC=CC=C(I)C(C)(C)C')
(5.60, 'CCC=CC=CC=CC=CC=CC=CC=CC=CC=CC=CC=CC=CC=CC=CC=CC(C)(C)CCC')
(5.44, 'CC=CC=CC=CC(Cl)=CC=CC=CC=CC=CC=C(C)C=CC=CC=C(C)C=CC(Br)=CC=CCCC')
(5.35, 'CC=CC=CC=CC=CC=CC=CC=CC=CC=CC=CC=CC=CC=CC=CC=CC=C(CC)C(C)C')
...
For QED optimization, the task initialization is as follows:
task = tasks.AutoregressiveGeneration(node_flow, edge_flow,
max_node=38, max_edge_unroll=12,
task="qed",
criterion={"ppo": 0.25, "nll": 1.0},
reward_temperature=10, baseline_momentum=0.9,
agent_update_interval=5, gamma=0.9)
The results are as follows:
(0.948, 'O=S(=O)(NC1=CC=CC=C1Br)C1=CC=CC=N1')
(0.947, 'CC1CCNC(C2=CC=CC=C2)N1S(=O)(=O)C1=CC=CC=C1')
(0.947, 'O=C(NCC1=C(Br)C=CC=C1F)C1=CC=CN=C1')
(0.947, 'COC1=C(C2=C(Cl)C=CC(S(N)(=O)=O)=C2)C=CC=C1')
(0.946, 'O=S(=O)(NC1=CC=CC=C1)C1=CC=C(Br)C=C1')
(0.945, 'O=S(=O)(NC1=CC=CC(Br)=C1)C1=CC=CC=C1')
...