Graph Neural Network Layers#
Modern graph neural networks encode graph structures with message passing layers and readout layers. In some cases, graph-to-node broadcast may also be needed. All these operations can be easily implemented with TorchDrug.
|
|
|
Message Passing Layers#
A message passing layer can be described as 3 steps, a message generation step, an aggregation step and a combination step. The \(t\)-th message passing layer performs the following computation
where \(h_i^{(t)}\) denotes node representations, \(m_{i,j}^{(t)}\) denotes messages from node \(j\) to node \(i\) and \(u_i^{(t)}\) is the aggregated messages, i.e., updates.
In TorchDrug, these steps are abstracted as three methods, namely
message(graph, input), aggregate(graph, message) and
combine(input, update).
Here we show an example of a custom message passing for PageRank algorithm. Representing the PageRank value as \(h_i^{(t)}\), one PageRank iteration is equivalent to the following functions.
We use the convention that \(degree\_in_j\) represents the degree of node \(j\) as the source node of any edge. The corresponding implementation is
from torch_scatter import scatter_add
from torchdrug import layers
class PageRankIteration(layers.MessagePassingBase):
def message(self, graph, input):
node_in = graph.edge_list[:, 0]
message = input[node_in] / graph.degree_in[node_in].unsqueeze(-1)
return message
def aggregate(self, graph, message):
node_out = graph.edge_list[:, 1]
update = scatter_add(node_out, message, dim=0, dim_size=graph.num_node)
return update
def combine(self, input, update):
output = update
return output
Let’s elaborate the functions one by one. In message(), we pick the source
nodes of all edges, and compute the messages by dividing the source nodes’ hidden
states with their source degrees.
In aggregate(), we collect the messages by their target nodes. This is
implemented by scatter_add() operation from PyTorch Scatter. We specify
dim_size to be graph.num_node, since there might be isolated nodes in
the graph and scatter_add() cannot figure it out from node_in.
The combine() function trivially returns node updates as new node hidden
states.
Readout and Broadcast Layers#
A readout layer collects all node representations in a graph to form a graph representation. Reversely, a broadcast layer sends the graph representation to every node in the graph. For a batch of graphs, these operations can be viewed as message passing on a bipartite graph – one side are original nodes, and the other side are “graph” nodes.
TorchDrug provides effcient primitives to support this kind of message passing.
Specifically, node2graph maps
node IDs to graph IDs, and edge2graph
maps edge IDs to graph IDs.
In this example, we will use the above primitives to compute the variance of node representations as a graph representation. First, we readout the mean of node representations. Second, we broadcast the mean representation to each node to compute the difference. Finally, we readout the mean of the squared difference as the variance.
from torch import nn
from torch_scatter import scatter_mean
class Variance(nn.Module):
def forward(self, graph, input):
mean = scatter_mean(input, graph.node2graph, dim=0, dim_size=graph.batch_size)
diff = input - mean[graph.node2graph]
var = scatter_mean(diff * diff, graph.node2graph, dim=0, dim_size=graph.batch_size)
return var
Notice that node2graph is used
for both readout and broadcast. When used in a scatter function, it serves as
readout. When used in a conventional indexing, it is equivalent to broadcast.
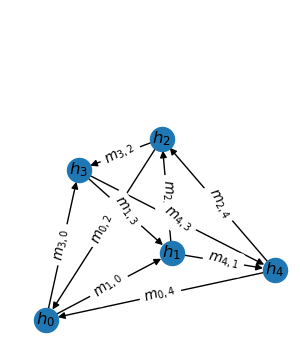 Message passing
Message passing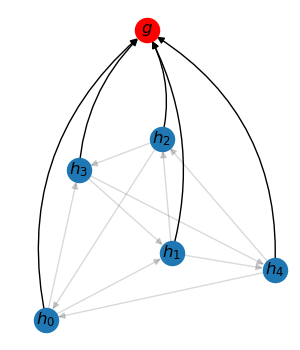 Node-to-graph readout
Node-to-graph readout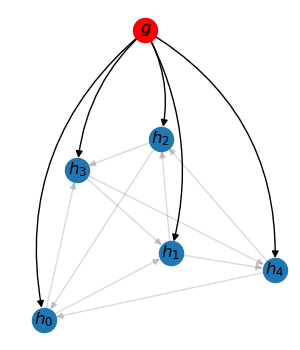 Graph-to-node broadcast
Graph-to-node broadcast